• 깊이 우선 탐색(Depth-First-Search)그래프 탐색 알고리즘임.
• 하나의 정점으로부터 시작해 차례때로 모든 정점들을 한 번씩 방문하는 것.
  • 정점은 Node or Vertex
• 재귀함수와 스택으로 구현이 가능.

알고리즘

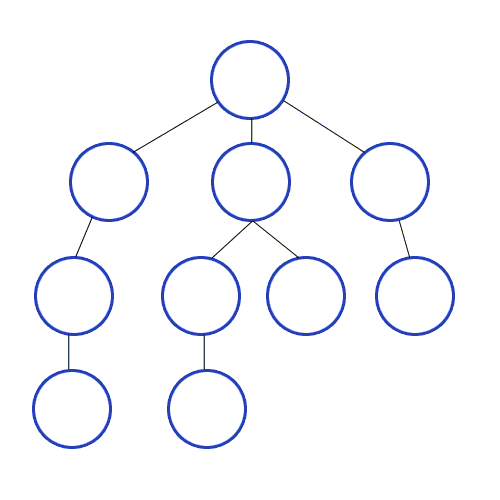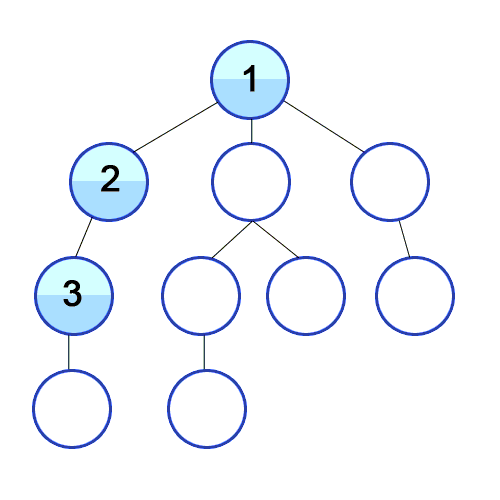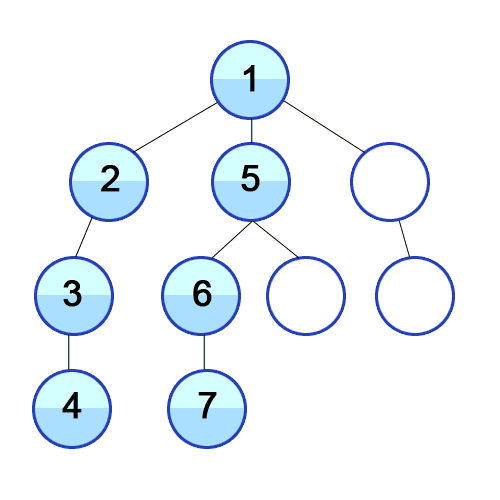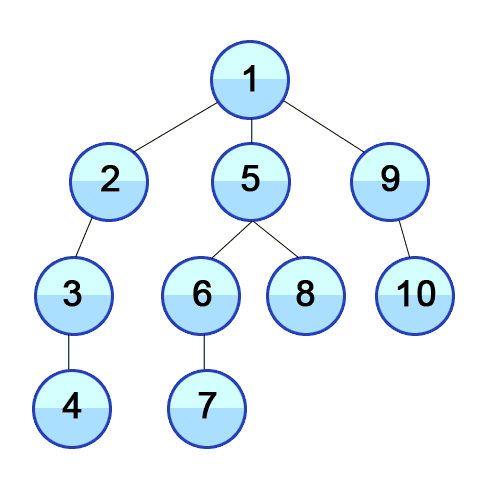
• 루트노드 or 임의의 노드에서 시작함.
• 다음 분기로 넘어가기 전에 해당 분기를 완벽하게 탐색함.
  • 1 → 2의 모든 간선을 탐색.
  • 2의 모든 간선 탐색을 완료했다면, 선택한 방문하지 않은 인접노드로 돌아가 위 로직을 반복.
    • 5, 9에 연결된 간선의 노드를 탐색.

소스코드 - Kotlin

fun main() {
    // 노드가 연결된 간선
    val graph = mapOf(
        1 to listOf(2, 3, 4),
        2 to listOf(1, 4),
        3 to listOf(1, 4),
        4 to listOf(1, 2, 3)
    )
    println("stack : ${dfsWithStack(1, graph)}") // 1, 2, 4, 3
    println("recursive : ${dfsWithRecursion(1, graph)}") // 1, 2, 4, 3
}

// 스택
fun dfsWithStack(start: Int, graph: Map<Int, List<Int>>) {
    val visited = mutableSetOf<Int>()
    val stack = Stack<Int>()

    stack.push(start)

    while (stack.isNotEmpty()) {
        val node = stack.pop()
        if (node !in visited) {
            println(node)
            visited.add(node)
            graph[node]?.reversed()?.forEach { 
                if (it !in visited) {
                    stack.push(it)
                }
            }
        }
    }
}

// 재귀
fun dfsWithRecursion(node: Int, graph: Map<Int, List<Int>>, visited: MutableSet<Int> = mutableSetOf()) {
    if (node in visited) return
    println(node)
    visited.add(node)
    graph[node]?.forEach { dfsWithRecursion(it, graph, visited) }
}

범위 및 함수 사용시 유의사항

• indices : IntRange타입을 반환하며**,** 수신객체의 전체 범위 반환. 위 예제 에선 0..6
• until : 범위의 마지막 요소를 포함하지 않음.
  • 0..5 => 0, 1, 2, 3, 4, 5
  • 0 until 5 => 0, 1, 2, 3, 4
• numbers.size , numbers.lastIndex 을 주의해서 사용.

장점

• 현 경로의 노드들만 기억하면 되므로, 저장공간의 수요가 비교적 적음.
• 목표노드가 깊은 단계에 있을 경우 해를 빨리 구할 수 있음.

단점

• 해가 없는 경로에 깊이 빠질 가능성이 있음.

시간 복잡도

• O(V+E)
  • 간선 + 노드